Moreau Envelope for Nonconvex Bi-Level Optimization: A Single-Loop and Hessian-Free Solution Strategy

Risheng Liu, Zhu Liu, Wei Yao, Shangzhi Zeng, Jin Zhang
Dalian University of Technology,Pazhou Laboratory (Huangpu),Southern University of Science and Technology,University of Victoria
ICML 2024
Paper Code Jittor Code arXiv

Abstract

This work focuses on addressing two major challenges in the context of large-scale nonconvex Bi-Level Optimization (BLO) problems, which are increasingly applied in machine learning due to their ability to model nested structures. These challenges involve ensuring computational efficiency and providing theoretical guarantees. While recent advances in scalable BLO algorithms have primarily relied on lower-level convexity simplification, our work specifically tackles large-scale BLO problems involving nonconvexity in both the upper and lower levels. We simultaneously address computational and theoretical challenges by introducing an innovative single-loop gradient-based algorithm, utilizing the Moreau envelope-based reformulation, and providing non-asymptotic convergence analysis for general nonconvex BLO problems. Notably, our algorithm relies solely on first-order gradient information, enhancing its practicality and efficiency, especially for large-scale BLO learning tasks. We validate our approach's effectiveness through experiments on various synthetic problems, two typical hyper-parameter learning tasks, and a real-world neural architecture search application, collectively demonstrating its superior performance.

To the best of our knowledge, this work is the first study to utilize Moreau envelope-based reformulation of BLO, to design a single-loop and Hessian-free gradient-based algorithm with non-asymptotic convergence analysis for general BLO problems with potentially nonconvex and nonsmooth LL objective functions:

  1. We propose the Moreau Envelope based Hessian-free Algorithm (MEHA), for general BLO problems with nonconvex and probably nonsmooth LL objective functions. MEHA avoids second-order derivative approximations related to the Hessian matrix and can be implemented efficiently in a single-loop manner, enhancing its practicality and efficiency for large-scale BLOs.
  2. We provide a rigorous analysis of the non-asymptotic convergence of MEHA under milder conditions, avoiding the need for either the convexity assumption or the PL condition on LL problem. In the context of the smooth BLO scenario, our assumption simplifies to UL and LL objective functions being L-smooth.
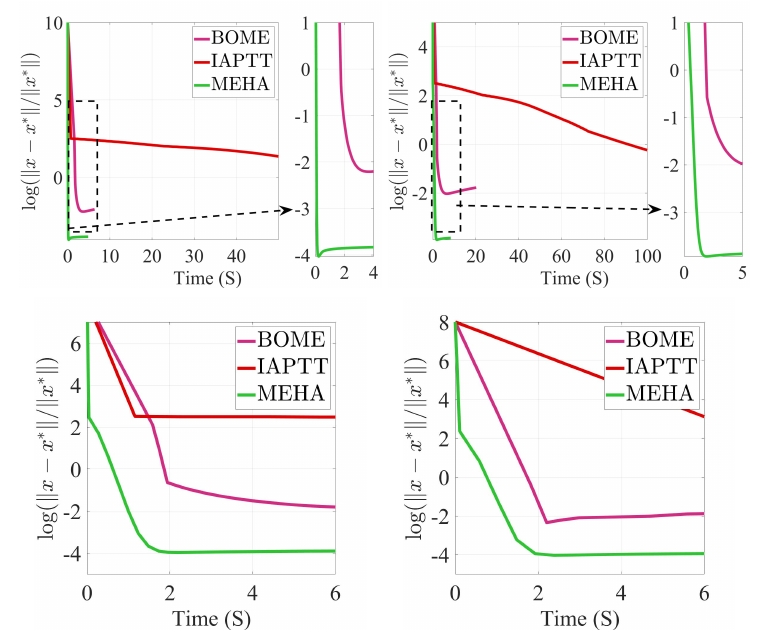
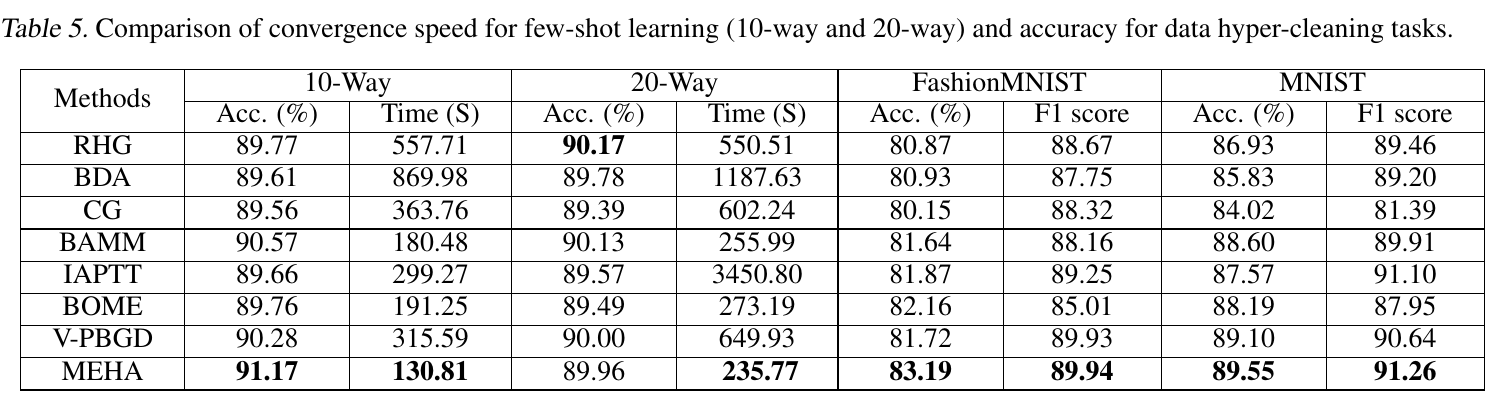
  3. We validate the effectiveness and efficiency of MEHA on various synthetic problems, two typicial hyper-parameter learning tasks and the real-world neural architecture search application. These experiments collectively substantiate its superior performance.

Moreau Envelope based Hessian-Free Algorithm (MEHA)

Synthetic Numerical Verification

In this section, we verify the convergence behaviors and applicable practicality of MEHA on a series of different synthetic problems. We compare the performance of MEHA with several Bi-Level Optimization (BLO) schemes (i.e., BOME, and IAPTT) across different dimensions in the below figure (LL non-covex case). Numerical comparisons, particularly the iterative time with advanced competitors in the following table. Our method MEHA achieves the fastest convergence speed, outperforming BOME.

Number of LoRAs for semantic convergence

Few-Shot Learning

The goal of N-way M-shot classification is to improve the adaptability of learnable model, facilitating rapid adaptation to new tasks. In our experiments using the Omniglot dataset, specifically in 10-way 1-shot and 20-way 1-shot scenarios with a LL convex formulation, we provide a runtime comparison in the below table to achieve consistent accuracy levels (90\%) for both scenarios. Notably, our method attains comparable accuracy while significantly reducing computational time.

Spectral DeTuning code

Neural Architecture Search

The main goal is to discover high-performance neural network structures. Our specific focus on differentiable NAS methods, representing a LL non-convex case. To showcase consistent performance, accuracy results are presented across different stages in the blow table. Remarkably, MEHA consistently outperforms specialized designs for NAS, establishing its superiority. These methods mostly require massive engineering to construct search strategies and spaces. MEHA based on BLO formulation can better improve the performances with theoretical guarantees.

Neural Architecture Search

BibTeX

@article{liu2024moreau,
  title={Moreau Envelope for Nonconvex Bi-Level Optimization: A Single-loop and Hessian-free Solution Strategy},
  author={Liu, Risheng and Liu, Zhu and Yao, Wei and Zeng, Shangzhi and Zhang, Jin},
  journal={ICML},
  year={2024}
}